Сумма внутренних углов выпуклого многоугольника является важной характеристикой в геометрии. Рассмотрим, как вычисляется эта величина для конкретного случая - двадцатисемиугольника.
Содержание
Сумма внутренних углов выпуклого многоугольника является важной характеристикой в геометрии. Рассмотрим, как вычисляется эта величина для конкретного случая - двадцатисемиугольника.
Общая формула для выпуклого n-угольника
Для любого выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (и углов) многоугольника.
Вычисление для 27-угольника
Подставляя n = 27 в общую формулу, получаем:
S = (27 - 2) × 180° = 25 × 180° = 4500°
Проверка правильности формулы
| Многоугольник | Формула | Сумма углов |
| Треугольник (n=3) | (3-2)×180° | 180° |
| Четырехугольник (n=4) | (4-2)×180° | 360° |
| Пятиугольник (n=5) | (5-2)×180° | 540° |
| 27-угольник (n=27) | (27-2)×180° | 4500° |
Вычисление одного угла правильного 27-угольника
Если 27-угольник правильный (все стороны и углы равны), то каждый внутренний угол (α) вычисляется по формуле:
α = (n - 2) × 180° / n = 4500° / 27 ≈ 166.67°
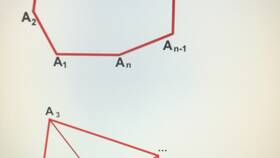
Геометрическое доказательство
- Выберем произвольную вершину 27-угольника
- Проведем диагонали из этой вершины ко всем несмежным вершинам
- Многоугольник разобьется на 25 треугольников (27 - 2)
- Сумма углов всех треугольников: 25 × 180° = 4500°
Свойства выпуклого 27-угольника
- Количество диагоналей: n(n-3)/2 = 27×24/2 = 324
- Сумма внешних углов (при обходе по часовой стрелке): всегда 360° для любого выпуклого многоугольника
- Каждый внешний угол правильного 27-угольника: 360°/27 ≈ 13.33°
Практическое значение
Хотя 27-угольник редко встречается в практических задачах, понимание принципов вычисления его углов важно для:
- Компьютерной графики и моделирования сложных фигур
- Архитектурных расчетов
- Теории графов и дискретной математики
- Кристаллографии
Историческая справка
Формула суммы углов многоугольника была известна еще древнегреческим математикам. Первые строгие доказательства появились в работах Евклида (III век до н.э.), хотя конкретные вычисления для многоугольников с большим числом сторон стали проводиться значительно позже.
Заключение
Сумма внутренних углов выпуклого двадцатисемиугольника равна 4500 градусов. Этот результат получен на основе общей формулы для выпуклых многоугольников и подтверждается геометрическими построениями. Понимание таких вычислений расширяет возможности работы с геометрическими фигурами любой сложности.
